Macrostructural models

2. Macrostructural models#

The economics profession uses a wide range of models for different purposes. Macro-structural models (also known as semi-structural or Macro-econometric models) are a class of models that seek to summarize the most important interconnections and determinants of economic activity in an economy. Computable General Equilibrium (CGE), and Dynamic Stochastic General Equilibrium (DSGE) models are other classes of models that also seek, using somewhat different methodologies, to capture the main economic channels by which the actions of agents (firms, households, governments) interact and help determine the structure, level and rate of growth of economic activity in an economy.

Typically, organizations, including the World Bank, use all of these tools, privileging one or the other for specific purposes. Macrostructural models like those that comprise the MFMod framework are widely used by Central Banks, Ministries of Finance; and professional forecasters to generate forecasts and to undertake policy analysis.

While macrostructural models fell out of favor with academic economists, they remain central tools in policy making and forecasting circles. In a series of discussions and papers Olivier Blanchard Blanchard [2018], former Chief Economist at the International Monetary Fund, concluded that academic economists are wrong to discard out-of-hand policy models such as macro-structural models. Those conclusions were reinforced in a recent collection of papers by leading academics Vines and Wills [2020] that argued that until a better framework could be developed, “policy-makers need to rely on structural economic models and the detailed econometric work which they embody” rather than the DSGE models favored by academics.

In this chapter - Macrostructural Models

This Chapter provides a high-level introduction to macro-structural models in general and the MFMod system in particular. It presents them as systems that balance theoretical rigor with practical utility, enabling comprehensive insights into economic systems. Macrostructural models are widely used by policymakers for scenario analysis and forecasting and MFmod is the main framework used by the World Bank for analyzing the economic progress and policies of developing economies.

It notes that these models are effectively a system of equations that describe the economic transactions (flow of funds) that occur in the economy, including those captured by the main economic accounting systems, including:

  • GDP and its subcomponents from the National Accounts expenditure, production, and income accounts.

  • Detailed government, monetary policy, and balance of payments accounts.

  • General equilibrium flow of funds linking households, firms, government, and foreign sectors.

The chapter introduces key concepts like:

  • Equation Types:

    • Identities: Accounting rules that always hold (e.g., GDP = C + I + G + X - M).

    • Behavioral Equations: Relationships based on economic theory, that are estimated econometrically and subject to error.

  • variable Types:

    • Exogenous Variables: Inputs determined outside the model, such as global oil prices.

    • Endogenous Variables: Variables determined by equations

The chapter also provides a brief description of ModelFlow the python package used to run World Bank models in an open source context.

2.1. A system of equations#

Mathematically, a macro-structural model is a system of equations comprised of two kinds of equations and three kinds of variables. Variables that are determined by an equation are classified by the type of equation that determines them, variables without an equation are deemed exogenous as they are determined outside of the model.

Models in the MFMod framework are comprised of:

  • Identities variables: that are determined by an identity: an equation that is a well-defined accounting rule that always holds. The famous GDP formula Y=C+I+G+(X-M) is one such identity, it indicates that GDP at market prices is definitionally equal to Consumption plus Investment plus Government spending plus Exports less Imports. The equation is an identity and the variable (Y in this instance) is also called an identity.

  • Behavioral variables that are determined by equations that attempt to statistically summarize the economic (vs accounting) relationship between variables, where the structure of the statistical relationship is derived from economic theory, but the sensitivities of different causal variables is estimated from the data. Thus, the neo-classical equation that says Real Consumption is determined by households maximizing their utility through the consumption of goods and services subject to a budget constraint is a behavioral equation. Because these behavioral equations only explain part of the variation in the variable they seek to explain, and because the sensitivities of variables to the changes in other variables are uncertain, these equations and their parameters are typically estimated econometrically and are subject to error.

  • Exogenous variables: do not have equations and are not determined by the model. Typically they are set either by assumption or from data external to the model. For an individual country model, the exogenous variables might include the global price of crude oil because the level of activity of a small economy itself is unlikely to affect the world price of oil. Similarly, the rate of growth of GDP in other economies may be treated as an exogenous variable, important to determining exports in the modeled developing country unlikely to be affected by activity in the modeled country (small country assumption).

Note

What dictates whether a variable is exogenous or endogenous is not set in stone. A variable that is exogenous in one model may be endogenous in another. For example in an single-country model, GDP growth of other countries may be exogenous, but in a multi-country model the GDP growth of those other countries would likely be endogenous (determined by the model).

Mathematically, a system of equations can be expressed as below:

\[\begin{align*} y_t^1 &= f^1(y_{t+u}^1...,y_{t+u}^n...,y_t^2...,y_{t}^n...y_{t-r}^1...,y_{t-r}^n,x_t^1...x_{t}^k,...x_{t-s}^1...,x_{t-s}^k) \\ y_t^2 &= f^2(y_{t+u}^1...,y_{t+u}^n...,y_t^1...,y_{t}^n...y_{t-r}^1...,y_{t-r}^n,x_t^1...x_{t}^k,...x_{t-s}^1...,x_{t-s}^k) \\ \vdots \\ y_t^n &= f^n(y_{t+u}^1...,y_{t+u}^n...,y_t^1...,y_{t}^{n-1}...y_{t-r}^1...,y_{t-r}^n,x_t^1...x_{t}^r,x..._{t-s}^1...,x_{t-s}^k) \end{align*}\]

where \( y_t^1 \) is one of n endogenous variables and \(x_t^1\) is one of k exogenous variables. To have a solution the system must have as many equations as there are unknown (endogenous variables).

Substituting the variable mnemonics Y,C,I,G,X,M for the y’s and x’s above, a simple macrostructural model can be written as as a system of 6 equations in 6 unknowns:

\[\begin{align*} Y_t &= C_t+I_t+G_t+ (X_t-M_t) \\ C_t &= c(C_{t-1},C_{t-2},I_t,G_t,X_t,M_t,P_t)\\ I_t &= i(I_{t-1},I_{t-2},C_t,G_t,X_t,M_t,P_t)\\ G_t &= g(G_{t-1},G_{t-2},C_t,I_t,X_t,M_t,P_t)\\ X_t &= x(X_{t-1},X_{t-2},C_t,I_t,G_t,M_t,P_t,P^f_t)\\ M_t &= m(M_{t-1},M_{t-2},C_t,I_t,G_t,X_t,P_t,P^f_t) \end{align*}\]

Where \(Y_t\) is an identity and \(C_t, I_t, G_t, X_t, M_t\) are behavioral variables and \(P_t, P^f_t\) (domestic and foreign prices, respectively) are exogenous in this simple model.

Such a system of equations can then be solved for the endogenous variables \(Y_t, C_t, I_t, G_t, X_t\) and \(M_t\) as a function of the exogenous variables in the system, notably as written above \(P_t\) and \(P^f_t\), and the estimated parameters and functional forms of the behavioral equations that link them, represented here by: \(c(), i(), g(), x()\) and \(m()\).

2.2. The MFMod Framework#

World Bank models are somewhat more complex and comprise many more sectors, notably:

  • GDP and sub components calculated from all three perspectives in Real, Nominal and implicit deflator terms

    • Expenditure Accounts

      • C + I + G + X - M

    • Production accounts (the level of detail varies from model to model)

      • Primary sector (Agriculture, Mining, Forestry)

      • Secondary Sector (Manufacturing, Industry)

      • Tertiary sector (Services, retail, Public Administration, Wholesale)

      • Energy sector (primarily broken out in climate models)

    • Income accounts (Wage Bill, Gross Operating surplus (Profits), Combined incomes)

  • Government Accounts

    • Revenues

      • Personal income taxes

      • Corporate income taxes

      • Value added taxes (Sales taxes)

      • Excise Taxes

      • Trade taxes (Export taxes, import duties)

      • Other taxes, (Fees and charges)

      • Grants and Transfers

    • Expenditures

      • Goods and services

      • Wages and salaries

      • Transfers to households

      • Subsidies to households

      • Subsidies to firms

      • Capital expenditures (New projects and repairs to existing capital stock)

      • Grants and Transfers

      • Interest payments on the debt

    • Balances

      • Overall fiscal balance

      • Primary fiscal balance

      • Debt (Domestic, Foreign)

  • Monetary Policy

    • Main policy rate

    • Money Supplies

    • International Reserves

    • Credit to the private sector

  • Balance of Payments

    • Current Account

      • Primary Exports and Imports (Merchandise and Services)

      • Secondary Exports and Services (Remittances, repatriation of profits, labor)

    • Financial Account

      • Equity financing

      • Debt financing

      • FDI

Within the models, these accounts are related in a general equilibrium flow of funds perspective, where households (as the owners of the factors of production) supply labor and capital to firms and the government via factor markets and earn salaries and profits paid for by the firms. Their earnings are spent on goods and services, taxes or saved, with their savings being intermediated through financial markets where they are either loaned to domestic firms, households and the government or to foreign firms and governments. Domestic households, firms and the government also lend to and borrow from the foreign sector. The output of firms is sold to households, the government or the rest of the world and the intermediate inputs they require are purchased from other firms, or the rest of the world.

Importantly every expenditure of a given actor in the economy is a revenue of another and, as a result, has impacts on the rest of the economy. This flow of funds idea is common to most macroeconomic models and is illustrated in the following schematic.

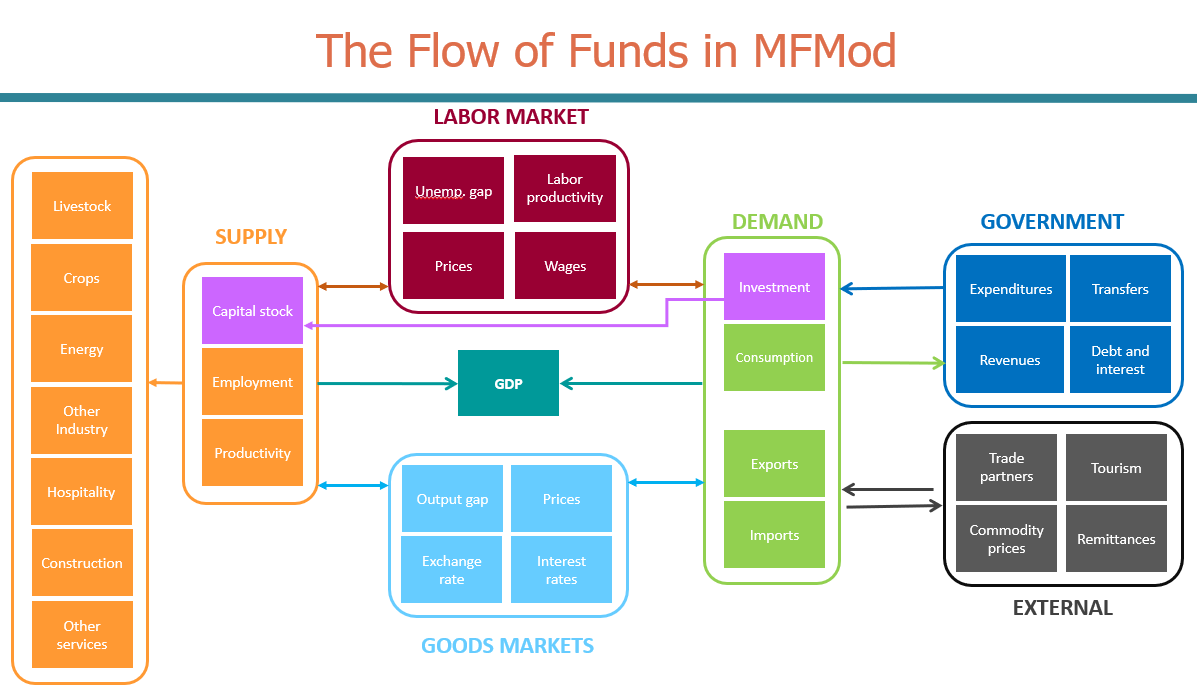
../../_images/FlowofFunds.png

Fig. 2.1 The Flow of funds in MFMod#

Contents